一维线性回归模型与梯度下降算法¶
课程大纲¶
本课程分为三个部分:
- 有监督的机器学习:回归与分类
- 高级学习算法
- 无监督的学习、推荐器、强化学习
监督学习与无监督学习¶
- 监督学习:有标签 \(y\),学 \(x \to y\) 的映射(回归/分类)。
- 无监督学习:无标签,发掘数据结构(聚类、降维、异常检测)。
线性回归模型¶
1) 任务与符号¶
- 训练集:\(\{(x^{(i)},y^{(i)})\}_{i=1}^m\)
- 单变量:\(x\in\mathbb{R}\);多变量:\(x\in\mathbb{R}^n\)
2) 假设函数¶
- 单变量: $$ f_{w,b}!\left(x^{(i)}\right)=w\,x^{(i)}+b $$
\[
\hat{y}^{(i)} = w\,x^{(i)} + b
\]
3) 成本函数(均方误差)¶
\[
J(w,b)=\frac{1}{2m}\sum_{i=0}^{m-1}\big(f_{w,b}(x^{(i)})-y^{(i)}\big)^2
\]
\[
J(w,b)=\frac{1}{2m}\sum_{i=0}^{m-1}\Big(\hat{y}^{(i)}-y^{(i)}\Big)^2
=\frac{1}{2m}\sum_{i=0}^{m-1}\Big(w\,x^{(i)}+b-y^{(i)}\Big)^2
\]
线性回归模型的思想是将训练集代入函数中,找出最小的 \(J(w,b)\) 所对应的 \(w,b\) 。 但是如何找出最小的 \(J(w,b)\) 呢?
梯度下降算法¶
有一种更系统的方法来找出w与b——梯度下降算法。梯度下降在机器学习中无处不在,不仅用于线性回归,还用于训练,例如一些深度学习模型。
梯度下降算法的思想:从一个初始点出发,沿着函数值下降最快的方向前进,直到到达局部最小值。用大白话来解释就是朝着最陡的方向下山。
1) 公式¶
\[
w = w - \alpha \,\frac{\partial}{\partial w} J(w,b)
\]
\[
b = b - \alpha \,\frac{\partial}{\partial b} J(w,b)
\]
等号表示赋值,α表示学习率。
2) 正确的做法¶
\[
\begin{aligned}
\text{tmp_w} &= w - \alpha\,\frac{\partial}{\partial w} J(w,b) \\
\text{tmp_b} &= b - \alpha\,\frac{\partial}{\partial b} J(w,b) \\
w &= \text{tmp_w} \\
b &= \text{tmp_b}
\end{aligned}
\]
意为同时更新w与b,在原始位置的基础上做梯度下降。
3) 学习率α¶
- α不能太小,也不能太大。 太小会导致收敛过慢,太大可能会导致错过最优解,甚至发散。
- 若J已达局部最小值,梯度下降会保持w不变。 因为此时梯度为0,更新公式变为 \(w = w - \alpha \cdot 0\),即 \(w\) 保持不变。
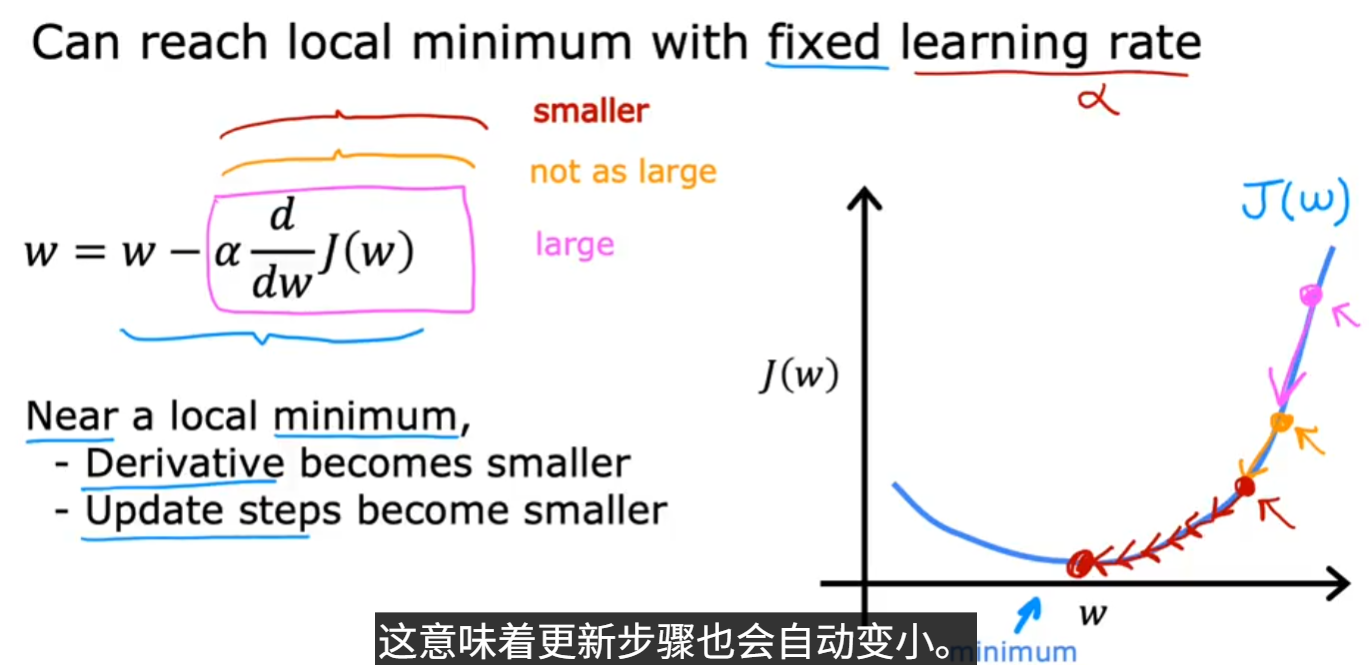
- 当J接近局部最小值时,导数会变得很小,下降的梯度也会变得很小,导致每次更新的步伐也变小,从而使得 \(w\) 的变化变得非常缓慢。 这是即使α是固定值成本函数J最终也能达到局部最小值的原因。
线性回归的梯度下降¶
1) 目标函数¶
\[
J(w,b)=\frac{1}{2m}\sum_{i=0}^{m-1}\Big(w\,x^{(i)}+b-y^{(i)}\Big)^2
\]
2) 梯度计算¶
\[
\frac{\partial}{\partial w} J(w,b) = \frac{1}{m}\sum_{i=0}^{m-1}\Big(w\,x^{(i)}+b-y^{(i)}\Big)x^{(i)}
\]
\[
\frac{\partial}{\partial b} J(w,b) = \frac{1}{m}\sum_{i=0}^{m-1}\Big(w\,x^{(i)}+b-y^{(i)}\Big)
\]
上方两式是用微积分推导出的,推导过程如下:
\[
\begin{aligned}
\frac{\partial}{\partial w}J(w,b)
&= \frac{d}{dw}\,\frac{1}{2m}\sum_{i=1}^{m}\!\left(f_{w,b}\!\left(x^{(i)}\right)-y^{(i)}\right)^{2}
= \frac{d}{dw}\,\frac{1}{2m}\sum_{i=1}^{m}\!\left(w\,x^{(i)}+b-y^{(i)}\right)^{2} \\[4pt]
&= \frac{1}{m}\sum_{i=1}^{m}\!\left(w\,x^{(i)}+b-y^{(i)}\right)x^{(i)}
= \frac{1}{m}\sum_{i=1}^{m}\!\left(f_{w,b}\!\left(x^{(i)}\right)-y^{(i)}\right)x^{(i)} \\[8pt]
\frac{\partial}{\partial b}J(w,b)
&= \frac{d}{db}\,\frac{1}{2m}\sum_{i=1}^{m}\!\left(f_{w,b}\!\left(x^{(i)}\right)-y^{(i)}\right)^{2}
= \frac{d}{db}\,\frac{1}{2m}\sum_{i=1}^{m}\!\left(w\,x^{(i)}+b-y^{(i)}\right)^{2} \\[4pt]
&= \frac{1}{m}\sum_{i=1}^{m}\!\left(w\,x^{(i)}+b-y^{(i)}\right)
= \frac{1}{m}\sum_{i=1}^{m}\!\left(f_{w,b}\!\left(x^{(i)}\right)-y^{(i)}\right)
\end{aligned}
\]
3) 更新规则¶
\[
\begin{aligned}
w &= w - \alpha\,\frac{\partial}{\partial w} J(w,b) \\
b &= b - \alpha\,\frac{\partial}{\partial b} J(w,b)
\end{aligned}
\]
w与b同时更新。
4) 线性回归的梯度下降算法¶
\[
w = w - \alpha \,\frac{1}{m}\sum_{i=1}^{m}\big(f_{w,b}(x^{(i)}) - y^{(i)}\big)\,x^{(i)}
\]
\[
b = b - \alpha \,\frac{1}{m}\sum_{i=1}^{m}\big(f_{w,b}(x^{(i)}) - y^{(i)}\big)
\]
-
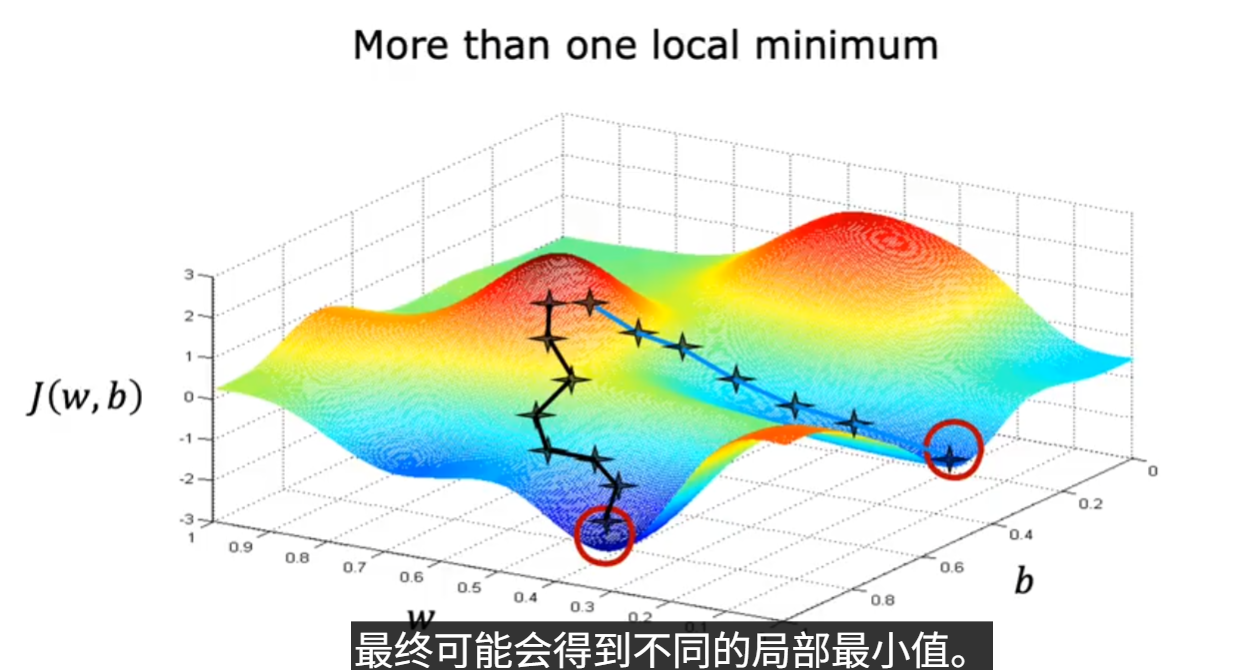
根据初始化参数w与b的不同,可能会得到不同的J的局部最小值。(如下图)
-
但是事实证明,线性回归的平方误差成本函数J是一个凸函数,所以不管初始化参数w与b为何值,最终都能收敛到同一个全局最小值。
这种梯度下降算法称为批量梯度下降(Batch Gradient Descent),因为每次迭代都使用了所有训练样本来计算梯度。
梯度下降算法的运行¶
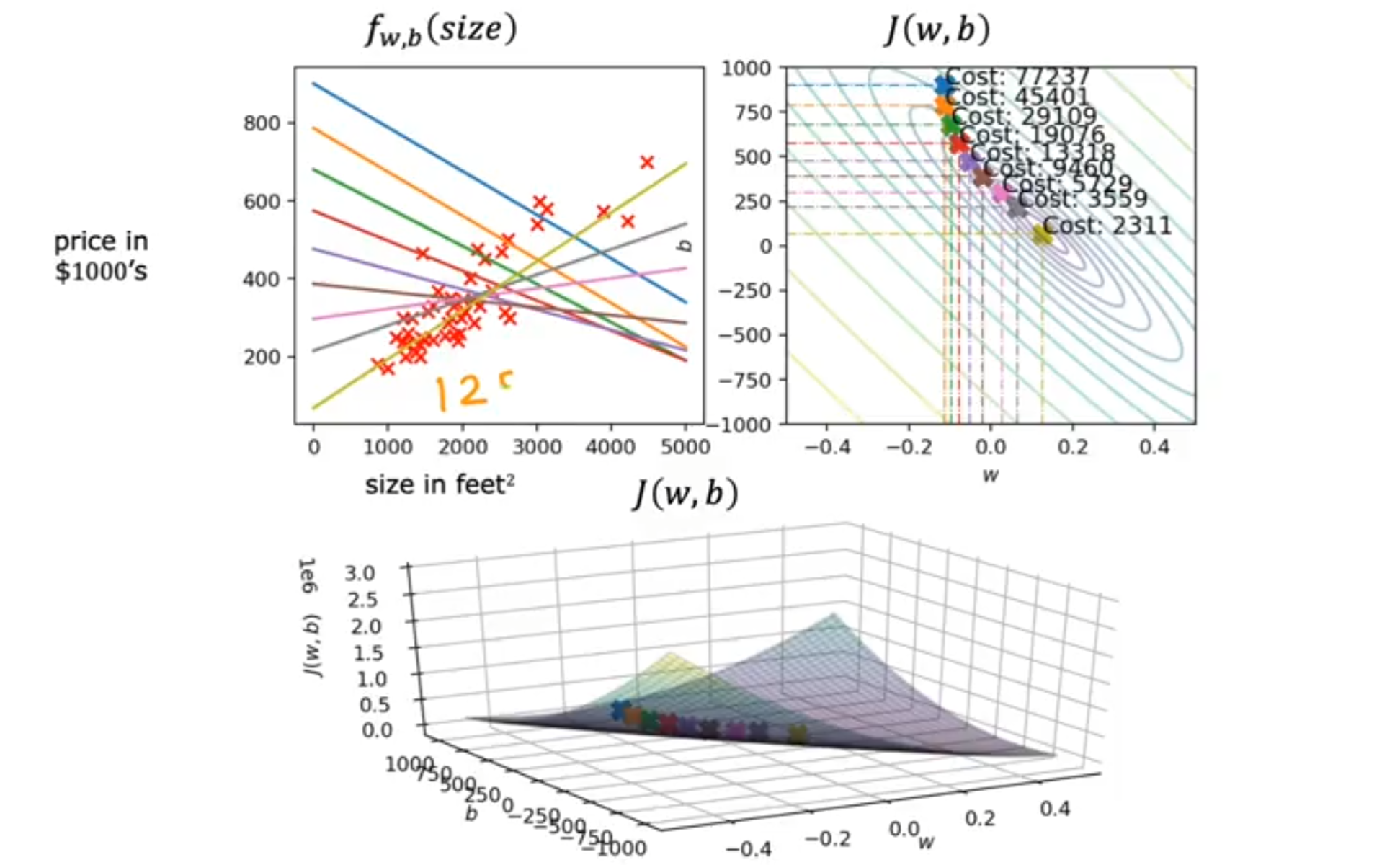
下图为演示实例,在本演示中初始化 w = -0.1 和 b = 900。
编辑于9月11日